Trigonometry Function Formulas
So, here are few Trigonometry Function Formulas. Let’s learn some basics of these formulas.
Trigonometry Function Formulas of a Right Triangle :
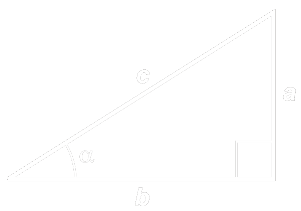
sin α = a / c = opposite / hypotenuse
cos α = b / c = adjacent / hypotenuse
tan α = a / b = opposite / adjacent
cot α = b / a = adjacent / opposite
sec α = c / b Cosec α = c / a
Basic Formula :
sin2 α + cos2 α = 1
tan α . cot tan α = 1
tan α = sin α / cos α = 1 / cot tan α
cot tan α = cos α / sin α = 1 / tan α
1 + tan2 α = 1 / cos2 α = sec2 α
1 + cot tan2 α = 1 / sin2 α = cos sec2 α
Trigonometric Table
| α | 00 | 300 | 450 | 600 | 900 | 1200 | 1800 | 2700 | 3600 |
| sin α | 0 | 1/2 | √2/2 | √3/2 | 1 | √3/2 | 0 | -1 | 0 |
| cos α | 1 | √3/2 | √2/2 | 1/2 | 0 | -1/2 | -1 | 0 | 1 |
| tan α | 0 | 1/√3 | 1 | √3 | ∞ | -√3 | 0 | ∞ | 0 |
| cot α | ∞ | √3 | 1 | 1/√3 | 0 | -1/√3 | ∞ | 0 | ∞ |
| sec α | 1 | 2/√3 | √2 | 2 | ∞ | -2 | -1 | ∞ | 1 |
| cosec α | ∞ | 2 | √2 | 2/√3 | 1 | 2/√3 | ∞ | -1 | ∞ |
Co-Ratios
| sin | cos | tan | cot | |
| -α | -sin α | +cos α | -tan α | -cot α |
| 900 – α | +cos α | +sin α | +cot α | +tan α |
| 900 + α | +cos α | -sin α | -cot α | -tan α |
| 1800 – α | +sin α | -cos α | -tan α | -cot α |
| 1800 + α | -sin α | -cos α | +tan α | +cot α |
| 2700 – α | -cos α | -sin α | +cot α | +tan α |
| 2700 + α | -cos α | +sin α | -cot α | -tan α |
| 3600k – α | -sin α | +cos α | -tan α | -cot α |
| 3600k – α | +sin α | +cos α | +tan α | +cot α |
Trigonometry Addition Formula:
- sin(A + B) = sinA cosB + cosA sinB
- sin(A – B) = sinA cosB – cosA sinB
- cos(A + B) = cosA cosB – sinA sinB
- cos(A – B) = cosA cosB + sinA sinB
- tan (A + B) = tanA + tanB / 1 – tanA tanB
- tan(A – B) = tanA – tanB / 1 + tanA tanB
- cot (A+ B) = cotA cotB – 1 / cotA + cotB
Product of Trigonometric Functions:
- sin α cos β = 1/2 [ sin (α + β) + sin(α – β)]
- cos α sin β = 1/2 [ sin (α + β) – sin(α – β)]
- cos α cos β = 1/2 [ cos (α + β) + cos(α – β)]
- sin α sin β = 1/2 [ cos (α – β) – cos(α + β)]
- tan α tan β = tan α + tan β / cot tan α + cot tanβ = – tanα – tan β / cot tan α – cot tan β
Trigonometric Formula with t = tan(x/2)
sinx = 2t / 1 + t2
cos x = 1 – t2 / 1 + t2
tan x = 2t / 1 – t2
cot x = 1 – t2 / 2t
Trigonometric Relation Between Functions:
Angle of a Plane Triangle :
- A, B, C are 3 angles of a triangle
- sin A + sin B + sin c = 4 cos(A / 2) cos(B/2) cos(C/2)
- cosA + cos B + cos C = 4 sin(A/2) sin(B/2) sin(C/2) + 1
- sinA + sinB – sinC = 4sin (A/2) sin (B/2) cos (C/2)
And, please visit this page to get more updates on Math Shortcut Tricks and Trigonometry Function Formulas. You can also like our facebook page to get updates.
So, if you have any question regarding Trigonometry Function Formulas then please do comment on below section. You can also send us message on facebook.



This is good?????
Intellegent
Sir me mathematics ka silvers chAiye
Please let these formulaes in easy way ..
And don’t expand it so much..
if n is a natural number .which is the solution to the equation tan(5a)=cot(3a)?
a=alpha symbol
5a = 90 – 3a
2a = 90
a = 45, then use the TanA = TanB formula to get the answer…
a belongs to (n(pi) +-(pi/2))
Nice formulaes
i like it……….
Nice but some formulas missing .
Disclaimer:
All contents of this website is fully owned by Math-Shortcut-Tricks.com. Any means of republish its content is strictly prohibited. We at Math-Shortcut-Tricks.com are always try to put accurate data, but few pages of the site may contain some incorrect data in it. We do not assume any liability or responsibility for any errors or mistakes in those pages. Visitors are requested to check correctness of a page by their own.