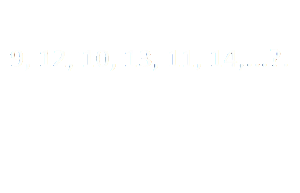Here in this section we will discuss some question and answer on Number puzzle which are very common in competitive exams. Without these type of Number puzzle question your exam preparation will not complete. To solve these questions you need to apply your math skills. Shortcut tricks can also be used to solve these Number puzzle questions.
Every types of Number puzzle problems and its shortcut tricks, how to do methods, you will find here in this website. Now apply shortcut tricks of Number puzzle in these problems to solve it. These questions can be solvable without using any shortcut methods also.
Now here we will give you a question on Number puzzle to solve. What you need to do is to, read the question carefully and then try yourself to solve the question. Answer will be provided below. If you solve the question then check your answer with our solution. You can also check below if you don’t know how to do the problem correctly.
Every page of this section is contain a question on Number puzzle with its detail explanation. By cliking on Next/Previous link you can navigate through other questions.
Let’s begin the Question answer session. Today’s question is:
What should be the number replaces in the question mark ?
To know the solution of this problem please scroll down below. You can take as much time as you need to solve the problem. But try to solve this question as quickly as you can.
(Scroll down to get the answer)
(Scroll down to get the answer)
(Scroll down to get the answer)
(Scroll down to get the answer)
Now answer of the above question will be discuss here. If you try the problem and got an answer then check your solution with us. If you got an correct answer then very Well Done, but don’t worry if you are unable to answer the previous question correctly. Now here is the solution of the problem with explanation.
You can solve in this way…………
first letter is added with 3 become = 9 + 3 = 12, then
subtruct 2 fr 12 that is 12 – = 10, again add 3 become 10 + 3 = 13 onwards. so question mark replaces with 12.
| << PREVIOUS QUESTION | NEXT QUESTION>> |
We provided some other questions on other topics also. Next/Previous link will get you through some other questions of different topics.
Please visit this page to get updates on more Math Shortcut Tricks and its uses.You can also like our facebook page to get updates.
If you have any question regarding this topic then please do comment on below section.You can also send us message on facebook.