Home > Math Shortcuts > Math Summation Notation

Math Summation Notation

Last Modified on by

Math Summation Notation

In mathematical formula it is indeed the addition of many number or variable which represent to give concise expression for sum of the variable as Sigma or Math Summation Notation.

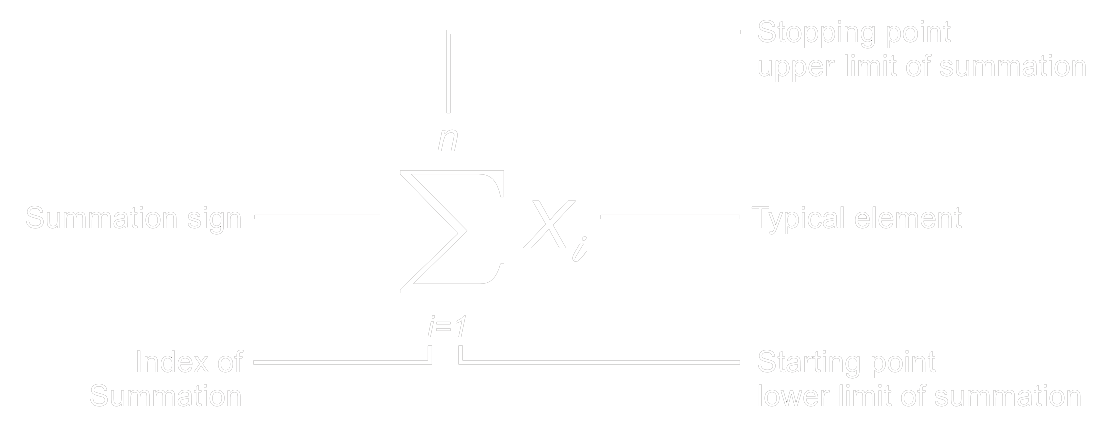
Math Summation Notation

 

\sum\limits_{i=1}^n i = \frac{n\left ( n+1 \right )}{2}

 

 

\sum\limits_{i=1}^n x_{i} This expressions shows that sum of values of x, which starting at x1 and it ending with xn .
\sum\limits_{i=1}^n x_{i} = x_{1} + x_{2} + x_{3} + … + x_{n}

 

\sum\limits_{i=1}^{10} x_{i} This expressions shows that sum of values of x, which starting at x1 and it ending with x10 .

\sum\limits_{i=1}^{10} x_{i} = x_{1} + x_{2} + x_{3} + x_{4} + x_{5} + x_{6} + x_{7} + x_{8} + x_{9} + x_{10}

 

 

\sum\limits_{}^{} x = x_{1} + x_{2} + x_{3} + … + x_{n}

 

 

\sum\limits_{i=1}^n x_{i}^{2} = x_{1}^{2} + x_{2}^{2} + x_{3}^{2} + … + x_{n}^{2}

This expressions shows that sum the squared values of x, which starting at x1 and it ending with xn.

 

 

 

Series Summation formula:

\sum\limits_{i=1}^n i^{1} = \frac{n\cdot \left ( n+1 \right )}{2}

 

\sum\limits_{i=1}^n i^{2} = \frac{n\cdot \left ( n+1 \right )\cdot \left ( 2n+1 \right )}{6}

 

\sum\limits_{i=1}^n i^{3} = \frac{n^{2}\cdot \left ( n+1 \right )^{2}}{4}

 

\sum\limits_{i=1}^n i^{4} = \frac{n\cdot \left ( 2n+1 \right )\cdot \left ( n+1 \right )\cdot \left ( 3n^{2}+3n-1 \right )}{30}

 

\sum\limits_{i=1}^n i^{5} = \frac{n^{2}\cdot \left ( 2n^{2}+2n-1 \right )\cdot\left ( n+1 \right )^{2}}{12}

 

\sum\limits_{i=1}^n i^{6} = \frac{n\cdot \left ( 2n+1 \right )\cdot\left ( n+1 \right )\cdot \left ( 3n^{4}+6n^{3}-3n+1 \right )}{42}

 

\sum\limits_{i=1}^n i^{7} = \frac{n^{2}\cdot \left ( 3n^{4}+6n^{3}-n^{2}-4n+2 \right )\cdot \left ( n+1 \right )^{2}}{24}

 

\sum\limits_{i=1}^n i^{8} = \frac{n\cdot \left ( 2n+1 \right )\cdot \left ( n+1 \right )\cdot \left ( 5n^{6}+15n^{5}+5n^{4}-15n^{3}-n^{2}+9n-3 \right )}{90}

 

\sum\limits_{i=1}^n i^{9} = \frac{n^{2}\cdot \left ( n^{2}+n-1 \right )\cdot \left ( 2n^{4}+4n^{3}-n^{2}-3n+3 \right )\cdot \left ( n+1 \right )^{2}}{20}

 

\sum\limits_{i=1}^n i^{10} = \frac{n\cdot \left ( 2n+1 \right )\cdot \left ( n+1 \right )\cdot \left ( n^{2}+n-1 \right )\cdot \left ( 3n^{6}+9n^{5}+2n^{4}-11n^{3}+3n^{2}+10n-5 \right )}{66}

 

* n = Number of terms

* i = Number sequence

 

 

 

<< Go back to Mathematical Formula

We provide few shortcut tricks on this topic. Please visit this page to get updates on more Math Shortcut Tricks. You can also like our facebook page to get updates.

If you have any question regarding this topic then please do comment on below section. You can also send us message on facebook.

Leave a Reply