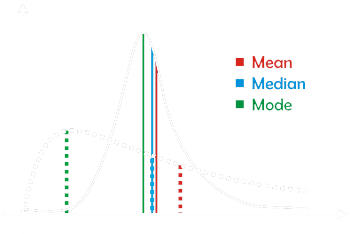
MEAN : The mean value is obtained the arithmetic mean or average of a set of numbers is expected value. The mean value is calculated by adding up all the values, and then dividing that sum by the number of values . Mean = Sum of all data values / Number of data values
Symbolically ,
Where (read as ” x bar”) is the mean of the set of x values, Σ x is the sum of all the x values, and n is the number of x values.
MEDIAN : The median is the middle value in a set of values. So to find the midian you need to order the numbers from largest to smallest and then you have to choose the value in the middle.
MODE : Mode is the value that the highest frequency in the data set.means values that occur most frequently and there can be more than one mode in a set.
numerical value that occurs most of the times. F (Xmode) = max
INTERSECTION : In intersection A ∩ B of two sets A and B is the set that contains all elements of B also belong to A (or similarly all elements of B that also belong to A) but no other elements. The symbol intersection is inverted U.
If Set A contain element A = {1,2,3} and set B contains B = {2,3,4} and the element in having common ares 2 and 3 and this intersection area formed a new set containing 2 and 3.
UNION :
The union of two sets A and B includes all elements which are members of either A or B. If sets A and B have any elements in common then this elements which are members of both sets are only include one in the union.
For example : If sets A contains the elements 1,2, and 3 and set B contains 2,3 and 4 the elements which are members of A or B are 1,2,3 and 4. This form a new set containing 1,2,3 and 4. when we write the union 2 and 3 are only listed once.
RELATIVE COMPLEMENT OF A IN B :
The relative complement of A in B denoted, B \ A, is the set of elements in B but not in A.
Symbolically :B \ A = {x | x ∈ B ∧ x ∉ A}
ABSOLUTE COMPLEMENT :
In a Set theory a complement of a set A refers to things not in A.
SYMMETRIC DIFFERENCE :
Operations on sets :
A ∪ A = A
A ∩ A = A
A ∪ B = B ∩ A
A ∩ B = B ∩ A
(A ∪ B) ∪ C = A ∪ (B ∪ C)
(A ∩ B) ∩ C = A ∩ (B ∩ C)
∪′ = ø
(A′)′ = A
A ∩ ø = ø
A ∩ U = A
A ∩ A′ = ø
(A ∪ B)′ = A′ ∩ B′
(A ∩ B)′ = A′ ∪ B′
We provide few tricks on Statistics Math Formulas. Please visit this page to get updates on more Math Shortcut Tricks. You can also like our facebook page to get updates.
If you have any question regarding this topic then please do comment on below section. You can also send us message on facebook.
If you have any questions or suggestions then please feel free to ask us. You can either comment on the section above or mail us in our e-mail id. One of our expert team member will respond to your question with in 24 hours. You can also Like our Facebook page to get updated on new topics and can participate in online quiz.
Disclaimer:
All contents of this website is fully owned by Math-Shortcut-Tricks.com. Any means of republish its content is strictly prohibited.
We at Math-Shortcut-Tricks.com are always try to put accurate data, but few pages of the site may contain some incorrect data in it. We do not assume any liability or responsibility for any errors or mistakes in those pages. Visitors are requested to check correctness of a page by their own.
this page has a nice tricks thanx