Mathematical Analytic Geometry

Mathematical Analytic Geometry

Mathematical Analytic Geometry is a coordinate system or branch of algebra that is used to model geometric objects like points, straight lines and circles angles in the Cartesian plane, the geometry shapes are defined as using coordinate system or algebric principles.

In this plane analytic geometry where points are represent as pairs of numbers like (x,y) and straight lines are defined as sets of points.

• A and B is two points and the distance between two points
• P = √( (x₂ – x₁) + ( y₂ – y₁))²
  
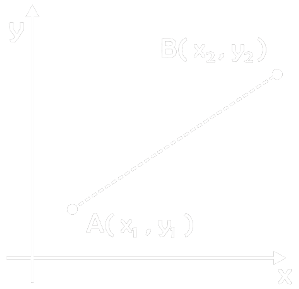
• P = √(x² + y²)

Triangle Analytic Geometry

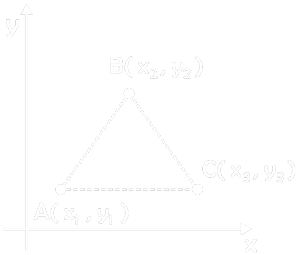
Area of Triangle with vertices at A, B, C

• A = ± 1 / 2 [(x₂ – x₁)(y₃ – y₁)(x₃ – x₁)(y₂ – y₁)]
•  = ± 1 / 2 [x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)]

Line Of Equation – Mathematical Analytic Geometry

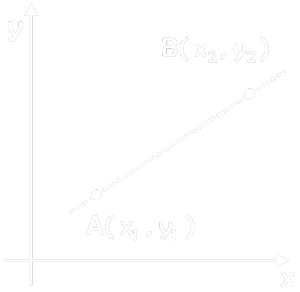
• A, B two points joining
• y – y₁ / y₂ – y₁ = x – x₁ / x₂ – x₁

Passing point A and parallel with line Y = ax + b

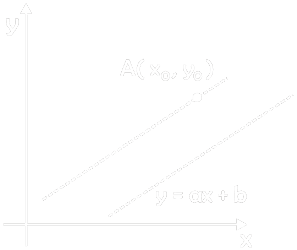
Passing A point  and perpendicular with line Y = ax + b

• y – y₀ = -1 / a (x – x₀)

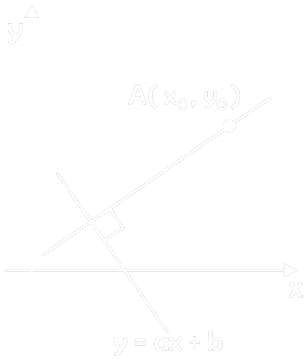
Equation Of Circle – Mathematical Analytic Geometry

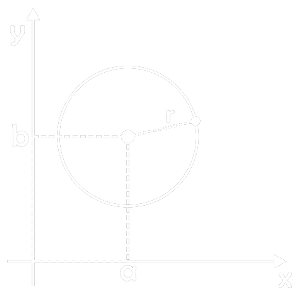
Radius of center is the form of the circle equation where circle with radius r and the center at (a,b)

• (x – a)² + (y – b)² = r²

The circle with center at origin

• x² + y² = r²

Ellipse – Mathematical Analytic Geometry

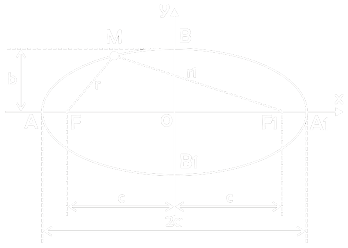
Equation Of Ellipse :

• Horizontal Major Axis :
  x² / a² + y² / b² = 1

• Vertical Major Axis :
  x² / b² + y² / a² = 1

• Eccentricity Ellipse :

ε = c / a = √(a² – b²)/ a < 1

• Area of Ellipse : A = πab

Hyperbola

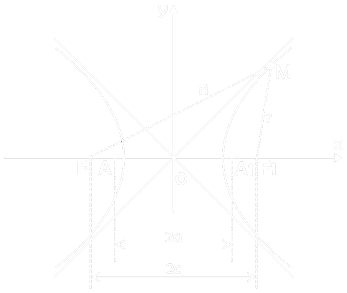
• Equation of Hyperbola :  x² / a² – y² / b² = 1
• Eccentricity Of Hyperbola : ε = c / a = √( a² + b² )/ a > 1

Parabola

• Area of Parabola : A = 2 / 3 lc
• Equation of Parabola : y² = 2px
• Eccentricity of Parabola : ε = FM / MK = 1

• << Go back to Mathematical Main page

We provided some other questions on other topics also. Click on the Next/Previous link to get more Question Answer session.

Please visit this page to get updates on more Math Shortcut Tricks and its uses.You can also like our facebook page to get updates.

If you have any question regarding this topic then please do comment on below section.You can also send us message on facebook.